4. sınıf sayı örüntüleri konu anlatımı ve konu özeti bu dersin içerğini oluşturmaktadır. Örüntü belli bir yapıyı, belli bir bütünü oluşturan dallardan, birimlerden her biri, örnek, biçim olarak tanımlanır. İlkokul 4.sınıf düzeyinde örüntüleri sabit artan , sabit azalan , artan , azalan, hem artan hem azalan örüntü şeklindeki başlıklarda inceleyeceğiz. Konu anlatımını soru çözümleri ile destekleyecek değişik soru tiplerine yer vereceğiz.

Sabit artan örüntü
Örüntüyü oluşturan sayıların artım miktarı her terimde benzerlik gösteriyorsa bu tip örüntülere sabit artan örüntü denir. Bu tipteki örüntülerin kuralını belirlerken örüntü kuralını üst tarafta belirtebiliriz. Bu örüntülerde örüntünün kuralı belirlendikten sonra sayı örüntüsünün hangi sayı veya sayılarla devam edeceğini bulmak için son terime artım miktarı eklenir. Örnek vermek gerekirse:
Soru: 7 – 14 – 21 – 28 – 35 – ? şeklinde verilen sayı örüntüsünün kuralını bulunuz. Örüntüde soru işareti ile gösterilen yere gelmesi gereken sayısı bulunuz.
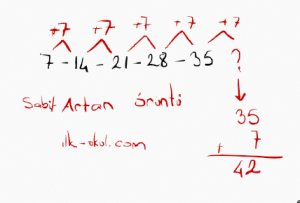
Kural: Yukarıdaki örnekte örüntü sabit bir şekilde artıyor. Artış miktarı yedi. Bu yüzden artım miktarlarını sürekli olarak yukarı kısma yazdık. Otuz beş sayısından sonra gelen sayıyı bulmak için de otuz beş ile yediyi topladık. Sonuç kırk iki oldu.
Soru: 7 – 10 – 13 – 16 – 19 sayı örüntüsü devam ettirilirse 6. ve 7. terimin çarpımı kaç olur?
Çözüm ve kural: Bu soruyu çözmek için ilk önce artım miktarını bulmamız gerekiyor. Her terimin artarak ilerlediğini görüyoruz. O zaman terimlerin üstlerine artım miktarlarını yazalım. Her terim üçer üçer artıyor. Demek ki 19’dan sonra gelen 6. ve 7. terim de üçer üçer artacak.
19 ile 3’ü toplarsak 22 eder( 5. terim)
22 ile 3’ü toplarsak 25 eder( 6. terim)
Altıncı ve yedinci terimlerin çarpımını soruyor. Çarpma işelmini yaparsak sonucu 550 buluruz.
Sabit azalan örüntü
Bu örüntü çeşidi sabit artan örüntüye benzerlik gösterir. Fakat bu sefer her terimde azalma görülür. Örüntüyü oluşturan sayıların azalma miktarı her terimde benzerlik gösteriyorsa bu tip örüntülere sabit azalan örüntü denir. Bu tipteki örüntülerin kuralını belirlerken örüntü kuralını alt tarafta belirtebiliriz. Sabit azalan sayı örüntüsünde, örüntünün kuralı bulduktan sonra örüntünün devamında gelecek sayıları bulmak için son terimden artım miktarı çıkartılır.
Soru: 50 – 45 – 40 – 35 – 30 – ? örüntüsünde soru işareti yerine gelmesi gereken sayı kaçtır?
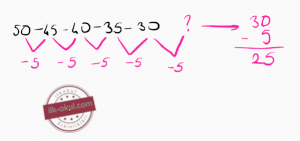
Kural: Soruya bakıldığı zaman terimler git gide azalıyor. Bu yüzden bu örüntü sabit olarak azalan örüntüdür. Azalma miktarlarını gördüğünüz gibi alt kısıma yazıldı. Azalma miktarı 5 olduğu için son terimden 5 çıkartıyoruz. Cevabı 25 buluyoruz.
Soru: 38 – 31 – 24 – 17 – ♥ örüntüsünde ♥ yerine hangi sayı yazılmalıdır.
Cevap ve kural: Örüntüde sayılar sürekli olarak azalıyor. Azalış miktarını bulmamız gerekiyor. Azalma miktarlarını terimlerin altlarına yazarsak yedişer yedişer azaldığını görürüz. O zaman son terimden yedi çıkartırsak ♥ yerine gelmesi gereken sayıyı buluruz. 17-7=10
Artan örüntü
Bir sayı örüntüsünde terimler arasındaki fark kurallı bir şekilde artıyorsa örüntüye artan örüntü denir. Sabit artan örüntüden farklı olarak artım miktarları değişiklik göstermektedir. Artan örüntüde kuralı bulmak için artış miktarı terimlerin üst bölümüne yazılır. Bir örnek olması açısından aşağıdaki örüntüyü inceleyebilirsiniz. Fotoğrafın altına örüntünün kuralını açıklayacağız.

Kural: Görüldüğü gibi örüntülerde sayılar artarak ilerlediği için artım miktarlarını üst bölüme yazdık. Örüntüde bir artış var fakat artış miktarları sabit değil. ilk önce 1 daha sonra 2 şeklinde bir artış var. En son terimde ise 6 artış göstermiş. Eğer örüntüyü devam ettirmek istersek sonraki terimin yedi artması gerekir.
Soru: 1- 2- 4- 7 – 11 – 16 – φ örüntüsünde φ ile gösterilen alana gelmesi gereken sayıyı bulunuz.
Cevap ve kural: Örüntüdeki terimler artış gösteriyor. Fakat her basamakta farklı artış miktarı mevcut. Bu artış miktarlarını terimlerin üstüne yazalım. 1 2 3 4 ve 5 olarak artmış. Demek ki en son basamakta 6 artış olacak. Yani son basamaktaki sayımız 22 olması gerekiyor.
Azalan örüntü
Bir sayı örüntüsünde, örüntüde yer alan terimler bir kural dahilinde azalıyorsa bu örüntüye azalan örüntü denir. Azalan örüntüde terimler arasındaki azalma miktarı örüntünün alt kısmına yazılır. Bu şekilde yaparsak örüntü kuralını daha kolay bulabiliriz. Haydi şimdi azalan örüntüyü bir örnek üzerinde inceleyelim. Örüntümüz 50 sayısından baslayacak.
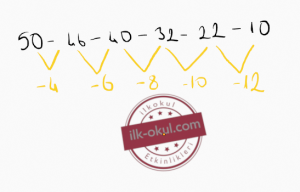
Kural : Örüntünün 50 sayısından başladığını söylemiştik. Sayıları incelediğimizde sayıların 4 6 8 10 12 şeklinde azaldığını görüyoruz. Artım miktarı artsa da önemli olan terimlerin azalmasıdır.
Hem azalan hem artan örüntü
Örüntüler bazı zamanlarda hem artış gösterirken hem de azalış gösterebilir. Bu artış ve azalışı inceleyerek örüntünün kuralını belirleyebiliriz. Örüntünün kuralını bulmak için azalma miktarlarını alt tarafa artış miktarlarını üst bölüme yazmalıyız. Aşağıda bazı örüntüler açıklanarak yazılmıştır. Kurallarına resmin altından ulaşabilirsiniz.
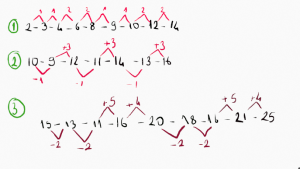
Açıklamalar:
1.Örnek: Örüntünün kuralı 2 kere bir arttır. 2 kere 2 arttır.
2.Örnek: Bir azalt 3 arttır.
3. Örnek: İki kere 2 azalt sonra bir kere 5 bir kere de 4 arttır.
Eğitsel Oyunlar
İlkokul etkinlikleri hızlı erişim sayfamızda eğitsel oyunlar sizi bekliyor. Online eğlenceli ve öğretici oyunlarla öğrendiklerinizi tekrar edin.
